No mercado financeiro em geral, muito se fala a respeito de gerenciamento de carteira, VaR (Value at Risk), CVaR (Conditional Value at Risk), entre muitas outras ferramentas quando tratamos de risco. Mas de que forma podemos aplicar tais teorias em mercados cuja volatilidade dos preços é tão elevada, como é o caso do Mercado Livre de Energia?
Antes de mais nada, é importante fixarmos alguns conceitos que serão base para o entendimento geral do tema. Para isso voltemos no tempo, especificamente para 1952, ano considerado como um divisor de águas na teoria de riscos, pois foi desenvolvida pelo economista norte americano Harry Max Markowitz, a Teoria Moderna do Portfólio (Teoria de Markowitz).
Esse foi o primeiro estudo a associar risco financeiro e a volatilidade dos retornos dos ativos, que renderia mais tarde, em 1990, o Prêmio Nobel de Economia para Markowitz. A Teoria Moderna do Portfólio possui três pilares: o retorno esperado de cada ativo, o risco e a correlação. A partir disso, um investidor poderia criar uma carteira de múltiplos instrumentos financeiros que maximizasse o retorno para um determinado nível de risco. Graficamente a linha que comporta o mix ideal desses ativos foi nomeada por Markowitz como fronteira eficiente.
Gráfico 1 - Fronteira Eficiente de Markowitz
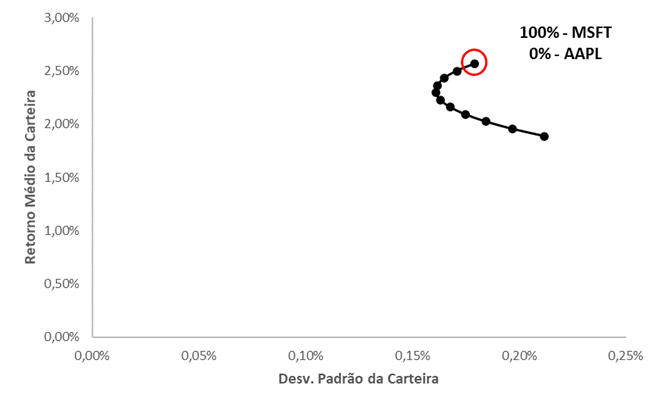
Fonte: Autor com os dados do Yahoo! Finanças
Para elucidarmos o conceito mencionado, montamos uma carteira de duas ações que compõem o S&P 500, Apple (AAPL) e Microsoft (MSFT). Baseado na teoria de Markowitz, a combinação ideal dos dois ativos seria composta apenas por ações da Microsoft, tendo em vista que investir exclusivamente nela apresentaria a melhor relação risco/retorno.
Com a evolução do mercado ao longo dos anos, novas técnicas de análise de risco foram sendo desenvolvidas, sendo o VaR uma das mais marcantes e utilizada até hoje. O conceito de “Valor em Risco”, foi introduzido em 1994 pelo banco J. P. Morgan & Co. e formalmente definido em 1997, pelo professor Philippe Jorion como “o valor que representa, para uma carteira ou ativo, a perda máxima esperada devida aos riscos de mercado para um período de tempo estabelecido e com dada probabilidade de ocorrência”.
Entretanto, assim como a maioria dos modelos matemáticos que são aplicados às finanças, o VaR foi desenvolvido inicialmente para mercados mais estáveis que assumia a normalidade dos retornos.
Gráfico 2 - Histograma da Distribuição dos Retornos do S&P 500
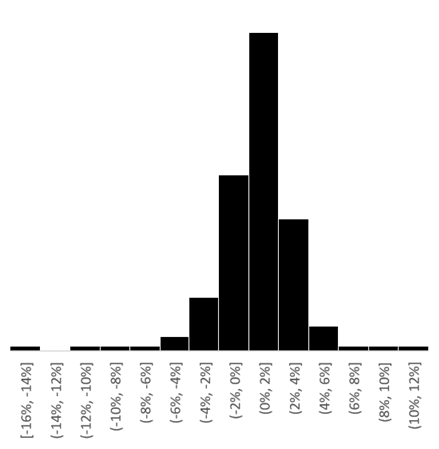
Fonte: Autor com os dados do Investing.com
Gráfico 3 - Histograma da Distribuição da Maturidade M+2 (Energia Elétrica)
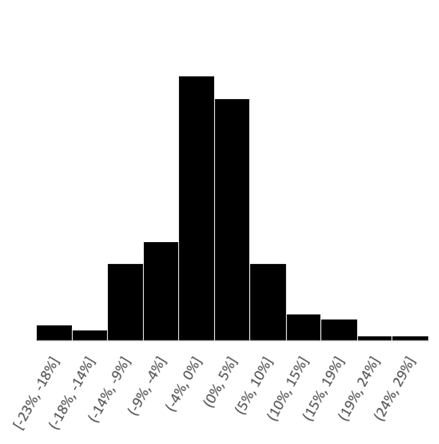
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Os gráficos acima ilustram a diferença entre as distribuições dos log-retornos semanais do S&P 500 e dos produtos de maturidade M+2 (produto com vencimento dois meses à frente) em energia elétrica, métrica muito utilizada para a mensuração do risco no mercado, uma vez que dessa forma conseguimos entender a correlação entre os diferentes vencimentos dos produtos. O gráfico 3, apresenta caudas mais relevantes (curtose) se comparado ao anterior, ou seja, as variações agressivas nos preços desse ativo são mais comuns, se distanciando de uma distribuição normal.
Existem algumas formas de estimar o risco de mercado para definir a perda máxima em um determinado portfólio, sendo as mais conhecidas:
Até aqui tivemos uma pequena introdução dos principais conceitos de risco e como eles podem ser aplicados em mercados que “fogem” de uma distribuição normal. Mas o que torna a energia elétrica um produto tão peculiar em termos de risco? Para isso, é preciso voltar aos três pilares da Teoria de Markowitz, que apesar de criada há 70 anos atrás, ainda serve como resposta para a maioria das questões acerca de risco financeiro.
Tabela 1 - Matriz de Correlação dos Produtos de Energia Elétrica por Maturidades

Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
O cálculo do risco em energia aplicado pelo método de Monte Carlo deve ter os produtos divididos por maturidades, sendo M+0 o mês atual, M+1 o próximo mês e assim por diante. Podemos utilizar quantas maturidades forem necessárias, porém o ideal é que a escolha das divisões de períodos apresente certa liquidez para que seja possível a elaboração de um banco de dados crível.
A partir do gráfico 2, pudemos perceber que o retorno esperado dos produtos de energia elétrica pode variar de forma bastante significativa e isso está diretamente atrelado ao modo como eles são precificados. Quanto à correlação dos ativos [Tabela 1], ela é positiva para todo e qualquer produto, isso significa que se o preço do M+2 começar a subir, o M+3 seguirá a mesma tendência ainda que de forma não proporcional, por exemplo. Essa relação ocorre, pois os preços de mercado são dados pelo compilado de todas as rodadas (cenários de preços gerados pelos modelos matemáticos que estipulam o PLD – Preço da Liquidação das Diferenças: preço o qual são liquidadas as posições mensais de cada agente do mercado) das comercializadoras de energia elétrica.
A construção desses diferentes cenários exige alto custo de oportunidade, bem como custos computacionais, considerando que análises mais assertivas e em menor espaço de tempo poderiam ser fA construção desses diferentes cenários exige alto custo de oportunidade, bem como custos computacionais, considerando que análises mais assertivas e em menor espaço de tempo poderiam ser feitas. Sendo assim, são realizadas rodadas das maturidades mais próximas M+1, M+2 e M+3 já que os dados de entradas são mais precisos e naturalmente o mercado assume que os produtos mais longos seguirão a mesma lógica. Para a simulação dos preços dos ativos de longo prazo, é necessário encadear todos os dados climatológicos dos períodos anteriores mesmo que eles ainda não tenham ocorrido, dessa forma as rodadas ficam sujeitas à uma sequência de erros.
Gráfico 4 - Volatilidade por Maturidade
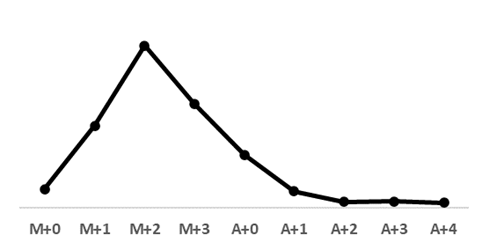
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
A volatilidade de cada uma dessas maturidades é outro ponto importante para destaque. Além da liquidez que está concentrada nos produtos mais curtos, existem também outros aspectos que explicam o gráfico 4. No M+0 as informações basicamente já estão dadas, dificilmente haverá uma mudança muito brusca em relação à previsão climatológica que impacte no preço desse produto. Por outro lado, nas maturidades intermediárias (M+1, M+2 e M+3) encontramos maior volatilidade devido às incertezas em relação as chuvas e previsões de carga (demanda de energia). No longo prazo (A+0 em diante), a volatilidade volta a cair pela falta de liquidez e por estar diretamente relacionado às mudanças estruturais como alteração no modelo de precificação, questões regulatórias, previsão de entrada de grandes geradores na pilha de despacho e/ou grandes consumidores que impacte na composição da carga do país.
Por último e não menos importante: o risco de mercado. Fundamento mais relevante quando aplicamos a Teoria de Markowitz no mercado de comercialização de energia elétrica. Derivado das variáveis pertencentes aos modelos de precificação (Newave, Decomp e Dessem), tem como objetivo otimizar a relação entre a utilização de geração hídrica, consequentemente tendo preços mais baixos de energia, e gerar com termelétricas com o intuito de preservar os reservatórios das hídricas, mas com preços mais altos.
As principais premissas desses modelos são as afluências previstas, tendo em vista que no Brasil a maior parte da capacidade instalada de geração de energia está nas hidrelétricas. Nesse primeiro momento já é possível identificar o potencial de variação no preço de energia dado que as afluências possuem natureza estocástica (o que também corrobora com a utilização da metodologia de Monte Carlo para a mensuração do risco), uma vez que estão ligadas à previsão de chuvas.
Ademais, outras variáveis impactam significativamente quando tratamos da volatilidade desse mercado e que também entram nos modelos. A carga, mudanças regulatórias e operação do sistema energético possuem um peso extremamente relevante conforme veremos em seguida.
Gráfico 5 - PLD Mensal do SE/CO (R$/MWh)
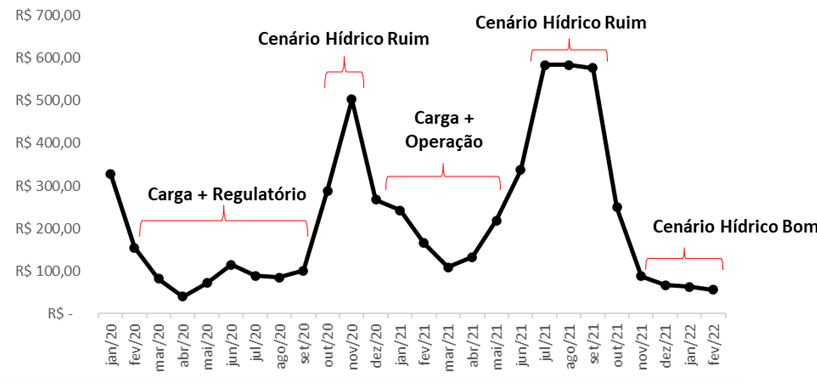
Fonte: Autor com os dados da CCEE (Câmara de Comercialização de Energia Elétrica)
A partir do gráfico 5 é possível identificar alguns períodos em que cada uma das variáveis citadas anteriormente impactou substancialmente nos preços de energia, contudo é notório que o peso de um cenário bom ou ruim de afluências é sempre mais significativo.
Gráfico 6 - Evolução diária do Preço de Mercado de Março/2020 no Subsistema Sudeste/Centro – Oeste (R$/MWh) para Energia Convencional
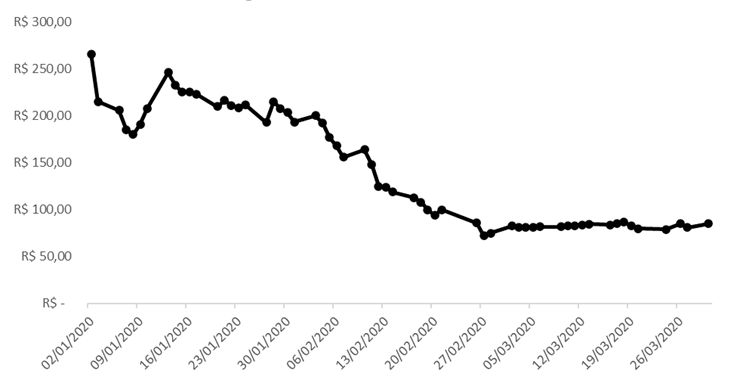
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Gráfico 7 - Evolução diária do Preço de Mercado de Novembro/2020 no Subsistema Sudeste/Centro – Oeste (R$/MWh) para Energia Convencional
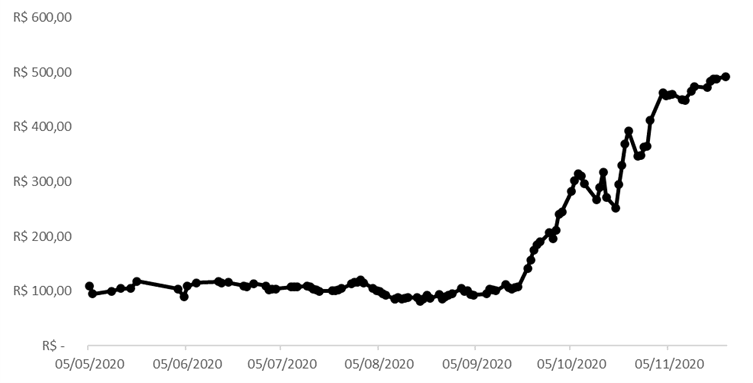
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Gráfico 8 - Evolução diária do Preço de Mercado de Março/2021 no Subsistema Sudeste/Centro – Oeste (R$/MWh) para Energia Convencional
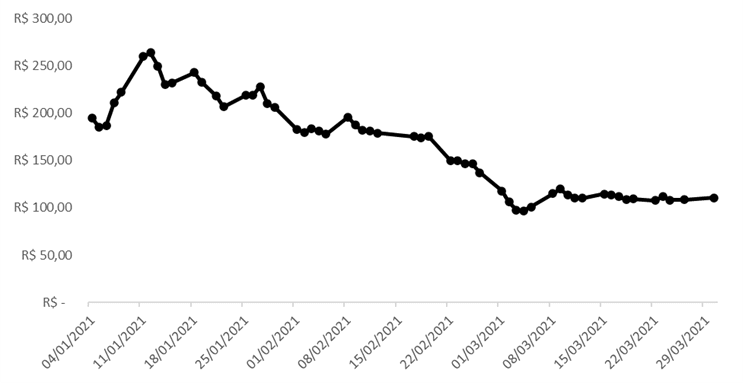
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Gráfico 9 - Evolução diária do Preço de Mercado de Julho/2021 no Subsistema Sudeste/Centro – Oeste (R$/MWh) para Energia Convencional
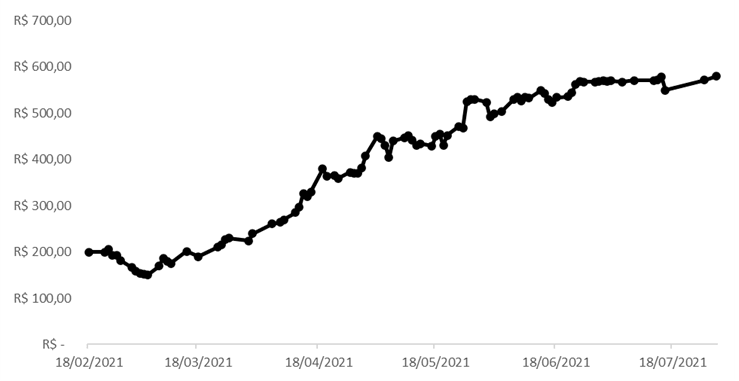
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Gráfico 10 - Evolução diária do Preço de Mercado de Novembro/2021 no Subsistema Sudeste/Centro – Oeste (R$/MWh) para Energia Convencional
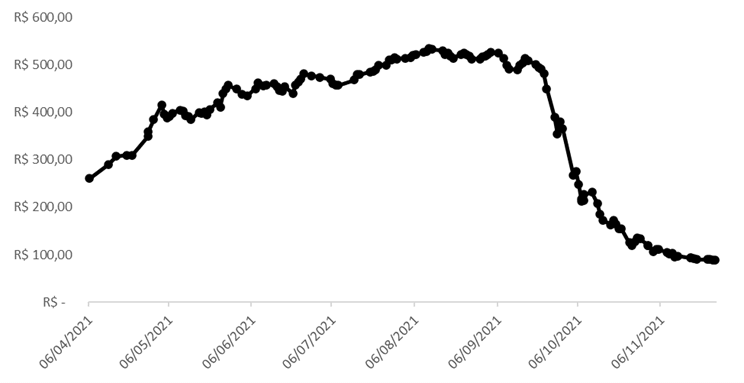
Fonte: Autor com os dados da BBCE (Balcão Brasileiro de Comercialização de Energia)
Para concluirmos, vamos analisar como o mercado foi respondendo à medida que cada uma das variáveis que citamos se confirmava. O gráfico 7 e 10 apresentam de maneira fiel toda a questão levantada até aqui. Em ambos, o mercado seguia em efeito platô, períodos em que há um consenso na direção da curva de preços, rumo ao piso ou teto. Entretanto, o principal “driver” dos modelos matemáticos que determinam o PLD segue sendo as afluências com variações imprevisíveis e aleatórias. Como consequência, existem diversos momentos em que, ao perceber uma mudança nas expectativas hidrológicas, o mercado reage rapidamente e de forma intensa.
Conforme citado anteriormente a metodologia que mais se adequa às peculiaridades do mercado é a aplicação do VaR sobre a Simulação de Monte Carlo, utilizando como processo estocástico o Movimento Browniano Geométrico (MBG). Essa ferramenta irá produzir diversos cenários aleatórios, respeitando a correlação entre as maturidades de cada produto e estipulando um intervalo de confiança no qual estará a perda máxima esperada da carteira.
Fato é que mesmo bastante aderente aos preços de energia elétrica, esse modelo de risco pode não ser capaz de capturar movimentos intensos quanto aos apresentados no gráfico 7 e no gráfico 10. Para isso, podem ser aplicados fatores de impulsão ou redução no desvio padrão dentro da fórmula do MBG:
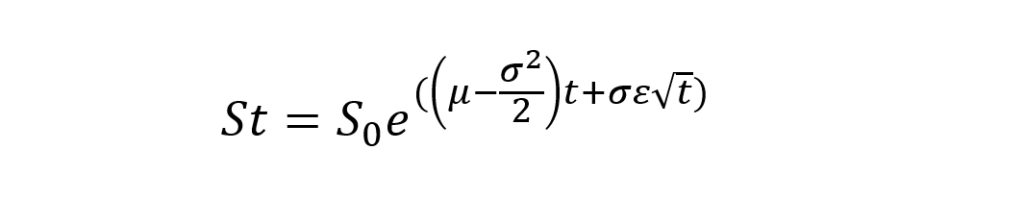
Note que no MBG o desvio padrão (σ) possui um caráter estocástico, uma vez que está multiplicando o épsilon (ε – variável aleatória), portanto o fator basicamente irá estressar ou atenuar os cenários. Com isso, conseguiremos obter valores que se encaixem com a realidade do mercado.
Em suma, apesar desse tipo de simulação ser a mais alinhada com o mercado de energia, dentre todas as apresentadas, é muito importante um estudo crítico dos resultados e não tê-los como verdade absoluta. Na prática, as equações devem ser usadas apenas para nortear as análises, principalmente sobre ativos que possuem quantidade relevante de risco não lineares como acontece em energia.
MAC499 - Trabalho de Formatura Supervisionado (usp.br)
https://ieeexplore.ieee.org/document/4202352/authors#authors
O que é Simulação de Monte Carlo? - Brasil | IBM
https://38285fd8-c043-4380-9729-1161c78ec3c1.usrfiles.com/ugd/38285f_559e8888394348cd9fad4b6a8b57b16d.pdf
SciELO - Brasil - Value-at-Risk da Carteira do Ibovespa: uma análise com o uso de modelos de memória longa Value-at-Risk da Carteira do Ibovespa: uma análise com o uso de modelos de memória longa
DDVargens.pdf (ufrj.br)
